3.0 Range Function¶

Calculating the Golden Angle with Loops 🌻¶

Plants exhibit beautiful patterns: from the branching patterns of trees, to the shapes of leaves, and the spiral patterns of a sunflower head. This last pattern, the spirals, arises from phyllotaxy (literally meaning “leaf” + “arrangement”). Phyllotaxy is more than just the arrangement of florets on a sunflower head, it is the arrangement of all lateral organs (leaves and flower parts). There are many more patterns than just spiral, but for this lesson and the next, let’s focus on spiral phyllotaxy and try to recreate the inspiring patterns on sunflower heads.

What is the Fibonacci sequence? And how is it related to the spiral patterns found in sunflowers and all plants? The Fibonacci sequence is a series of numbers that begins with 0, 1 or 1, 1. After the first two numbers, each consecutive number is the sum of the previous two. So, from 0, 1 the sequence of 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . . arises.

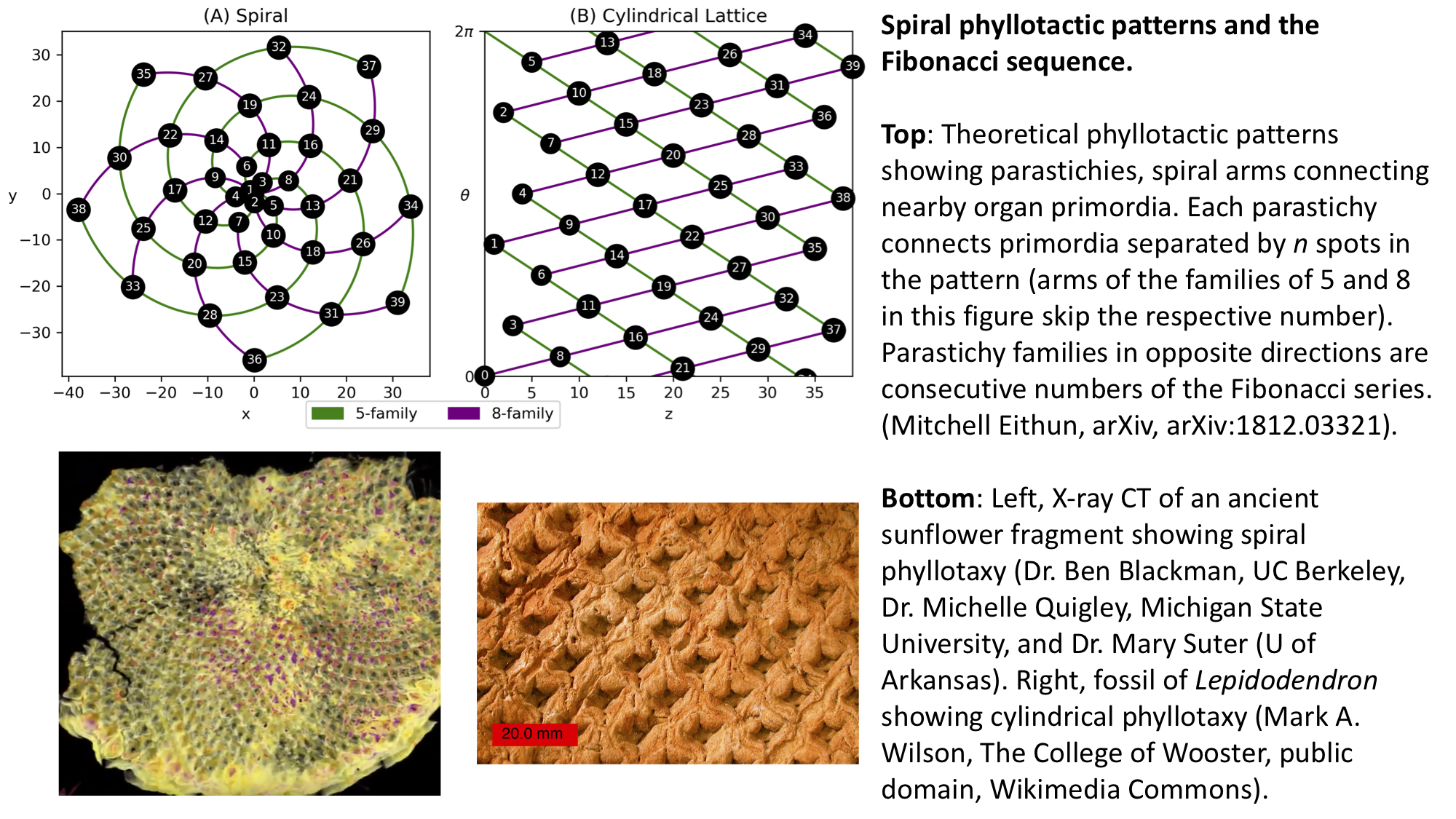
When looking at a sunflower head, a spiral phyllotactic pattern that is projected onto a disc, spiral arm patterns emanating from the center emerge. These are called parastichies, and arise from nearby neighbors in the overall phyllotactic pattern that are separated by n sequential primordia, where n is a term of the Fibonacci sequence.

For example, in a parastichy family of 5, the spiral arises from connecting every 5th primordium. One of the strongest connections between phyllotaxy and the Fibonacci sequence is that the parastichy families going in opposite directions are consecutive numbers of the Fibonacci sequence.

But the connection between the Fibonacci sequence and spiral phyllotaxy is even closer than parastichy families. The Golden Ratio is approximated by the ratio of two consecutive Fibbonaci numbers and becomes more accurate the farther in the sequence. The value of the Golden Ratio is $$\varphi=\frac{1 + \sqrt{5}}{2}\approx1.61.$$

If the circumference of a circle is divided into two arcs the ratio of the lengths of which form the Golden Ratio, the resulting angle is called the Golden Angle. The value of the Golden Angle is

\[\pi(3 - \sqrt {5})\;\text{radians or } 180(3 - \sqrt{5})\approx137.5^\circ.\]

The value of the angle between successive primordia in spiral phyllotaxy is the Golden Angle.

In this lesson we will be approximating the values of the Golden Ratio and Golden Angle using loops. In the next activity, we will use the Golden Angle value to recreate a sunflower head.

Looping towards the Golden Ratio¶

Computers are really good at doing repetitive tasks. A loop is one of the primary ways we tell a computer to perform a piece of code over and over again.

Loops come in two flavors:

for loops
while loops

A for loop will iterate over a piece of code for a specified number of times. A while loop will keep iterating over a piece of code while a condition is true.

It is not strictly true that the loop is simply repeating the same thing over and over again. Rather, it is iterating over an index. An index is a count of how many times the loop repeated, 0, 1, 2, 3, . . . (remember, all indexing starts with 0 in python). The index is a value that we use to vary, with each iteration, what the loop does. The index might be what we are after, simply a count that continues upwards by +1 with each iteration. Or, we use the index to get after other values. For example, the index of a loop might be used to iterate over the elements of a list, which might be any values that we choose. We might perform a mathematical function on each value of the loop index to transform it into another set of values we need.

Two common ways to iterate over a loop are using the range() function or just a list. The range() function takes a start, stop, and step value, or just the stop value by itself. For example, range(2,10,3) would yield 2,5,8, starting at 2 at adding 3 for each step until stopping at a value less than but not equal to 10. You an also just provide a stop value to range. For example, range(3) would yield 0,1,2. It is important to remember with range() that the start is inclusive and the stop is exclusive.

for loops have a strict structure, in which an arbitrary iterable variable name is provided and a set of values to iterate that variable over. The first line ends in a : and the code within the loop is indented. Python is sensitive to both the : and the indented white space, so these must be used to successfully use a for loop. For example:

for i in range(start, stop, step):
    # Your code here, but let's use print() as an example
    print(i)
    
for val in my_list:
    # Your code here, but let's use print() as an example
    print(val)

Unlike a for loop, a while loop will keep on iterating while a condition is true and stop iterating when it is no longer true. One common way to structure a while loop is to add a counter. A counter is a variable outside the loop that will increase its value every time the loop runs. We set the while loop to run until the counter exceeds a certain value. The counter increases in value using the += sign, which is equivalent to counter = counter + 1 in the example given below. One way to think about += is that it adds a value to the previous value of the counter to arrive at a new value of counter.

An example of a while loop with a counter is given below:

counter = 0

while counter < 20:
    # Your code here, but let's use print() as an example
    print(counter)
    # The code below increases the counter value by 1 each time the loop iterates
    counter += 1

It is worth investing time in understanding loops: they are a key element of coding in Python! Loops become very powerful when used smartly with the code within them, and also by creating values and lists outside the loops that the loops modify as they run.

Pay attention to the way that loops are used in the video tutorial below, and how they can be used to calculate something like the Fibonacci sequence.

🐍 Python learning objectives¶

The range() function and how it produces a series of integers to iterate over in a loop (1:20)
How to write a for loop (2:40)
How to use the += sign as a counter (7:25)
How to create an empty list outside of a loop and fill it with loop outputs (13:09)
How to use a for loop to calculate the Fibonacci sequence (20:33)
How to write a while loop using a counter (26:29)

🌻 Plant learning objectives¶

Plants are computers!
They iteratively produce outputs (like leaves and flowers), just like loops do
Modeling tries to recapitulate phenomena in nature. No model is perfect.
The Golden angle that plants use and we will calculate is based on computational mathematics
We will use sunflowers and the Golden angle as inspiration to learn from plants.

The `range()` function and how it produces a series of integers to iterate over in a loop¶

Watch this video from 0:00 to 2:35

# To load the video, execute this cell by pressing shift + enter

from IPython.display import YouTubeVideo
from datetime import timedelta
start=int(timedelta(hours=0, minutes=0, seconds=0).total_seconds())
end=int(timedelta(hours=0, minutes=2, seconds=35).total_seconds())

YouTubeVideo("Cvi3dByz9SE",start=start,end=end,width=640,height=360)

The following is a transcript of the video.

So let’s get started. We’ll start with the range() function and how it’s used to produce a series of integers that we iterate over in a loop.

This is a good time to go over the help function. If you’re ever in doubt about what a function is, you can just write a question mark in front of it. If we hit shift + enter we see we get a little help box. It’s not necessarily so helpful, but it will try to tell you something. So for example, we can see that the inputs to the range function are start, stop, and step. This is a lot like indexing and slicing that you learned about before and it says it returns an object that produces a sequence of integers from start, inclusive, to stop, exclusive, by step. And this almost sounds exactly like indexing and slicing that you learned about before.

# What is the range() function?
# If ever in doubt, use the help function with a "?"

?range 

# range(start, stop[, step]) -> range object
# Return an object that produces a sequence of integers
# from start (inclusive) to stop (exclusive) by step.  
# range(i, j) produces i, i+1, i+2, ..., j-1
# start defaults to 0, and stop is omitted! 
# range(4) produces 0, 1, 2, 3
# These are exactly the valid indices for a list of 4 elements
# When step is given, it specifies the increment (or decrement)

So based on that let’s try to execute a range() function. Let’s put in the number eight. Maybe based on our indexing before you would expect it to give you back zero, one, two, three, 4, 5, 6, 7, and that’s not what it gives us. Instead it just gives us range 0 to 8 which is kind of what we would expect based on just putting 8 there. And so this is a little unexpected.

So let’s explore more, and as you’ll see range() only works really in the context of a loop.

# So let's try out the range function!

print(range(8))

range(0, 8)

Welcome / Bienvenid@ 3.1 For Loops

Plants & Python