Contents

Practice with Calculating the Golden Angle with Loops 馃尰露

From the Fibonacci sequence to the Golden Ratio露

After watching the video tutorial, in the cell below, create a for loop that calculates the first 100 numbers of the Fibonacci sequence.

Do the following:

  • Remember to create a list outside your for loop to store your sequence. Call the list fibonacci

  • Remember that you need to specify the first two numbers of the sequence (0 and 1) in your list to calculate subsequent terms

  • You need to begin iterating on the 3rd element (index = 2) of your list to calculate the sequence

  • Each element of the sequence is the sum of the i-2 and i-1 elements

# Put your answer here

In the cell below, use the len() function to calculate the length of your list fibonacci (it should have 100 elements. If not, modify your loop to make sure this is the case).

# Determine the length of your Fibonacci list here:

Now that you have successfully made a loop to calculate the Fibonacci sequence, let鈥檚 modify your code to calculate the Golden Ratio, \(\varphi\)!

Calculating the Golden Ratio is easy if you have already calculated the Fibonacci sequence. The Golden Ratio is approximated by the ratio of element i divided by element i-1 of the Fibonacci sequence. The approximation of the Golden Ratio i/(i-1) becomes more accurate further in the series with larger numbers. Let鈥檚 use our loop making skills to approximate the Golden Ratio!

Copy and paste your Fibonacci sequence code from above. In the cell below, modify your code to do the following:

  • In addition to your Fibonacci list (pre-populated with 0 and 1 to calculate the sequence) add another empty list outside the loop called phi to store your approximations of the Golden Ratio

  • This time, let鈥檚 only calculate 52 elements of the Fibonacci sequence and 50 elements of phi. You still have to begin on the 3rd element (index = 2) to calculate the Fibonacci sequence, so you should add two extra iterations to make sure you get all 50 approximations of phi (because unlike the Fibonacci sequence, this list starts without any members).

  • In the for loop, still calculate each element of the Fibonacci sequence as the sum of (i-2) + (i-1) elements and append to the Fibonacci list

  • Add within your for loop a calculation of phi as i/(i-1) elements of the Fibonacci sequence

  • Important: in order for you to calculate phi as described above, the ith element of your Fibonacci list doesn鈥檛 exist until you calculate it! Be sure to calculate the next Fibonacci number of the series and append it to your list before you calculate phi. Fibonacci first, then phi.

# Put your answer here

In the cell below, print out:

  1. The len() of your list phi

  2. Print your list phi. Your list should approximate the value of the Golden Ratio: 1.618033988749895

# Put your answer here

From the Golden Ratio to the Golden Angle露

The beautiful spiral phyllotaxy of sunflowers and the lateral organs of other plants arises from the Golden Angle. The Golden Angle is derived from the Golden Ratio. If two arcs on a circle are defined such that the length of arc a divided by arc b is the Golden Ratio, then the resulting angle is the Golden Angle. As we just saw, the Golden Ratio is a product of the Fibonacci sequence, and this is how the inspiring patterns seen in a sunflower disc are linked to the Fibonacci sequence! 馃尰

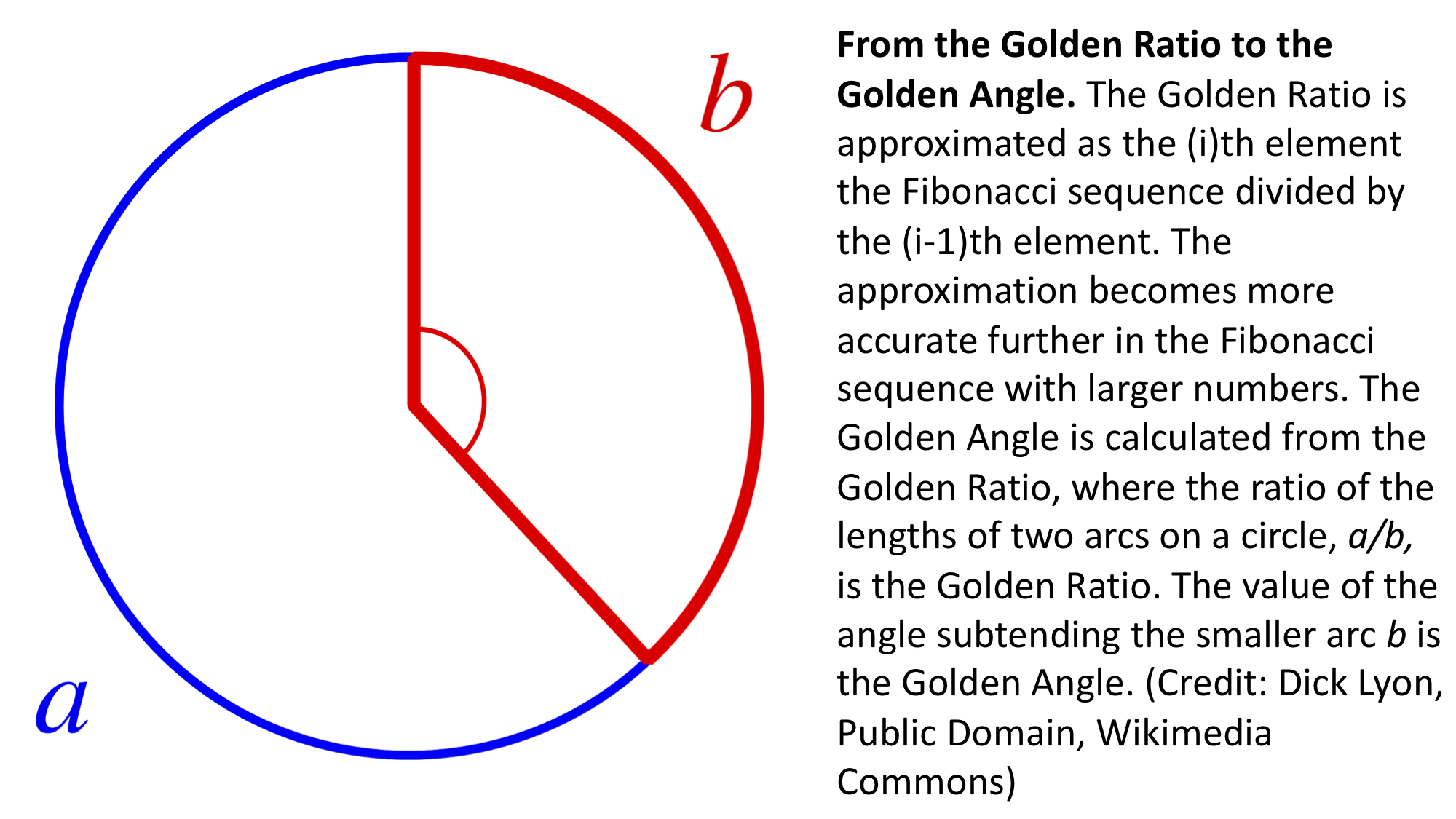
golden_angle.jpg

To approximate the Golden Angle, let鈥檚 figure out a way to calculate it from the Golden Ratio, as we already know how to do that!

But first, let鈥檚 get our most accurate estimation of the Golden Ratio.

In the next lesson, we will be using a function called .pop(). .pop() added to the end of a list will return the last element of the list. As the last member of our list phi is the best approximation of the Golden Ratio that we have, let鈥檚 use .pop() to get that value! The way you use .pop() is as follows:

my_variable = my_list.pop()

In the cell below, create a new variable called golden_ratio by using .pop() to isolate the last value of the list phi. Print out the value of golden_ratio.

# Put your answer here

The Golden Ratio has some very interesting properties.

In the cell below, print() the following using your new variable golden_ratio:

  • Print the value of golden_ratio

  • Print the value of golden_ratio squared

  • Print the value of 1 / golden_ratio

What do you observe that is similar between all the values that you just calculated?

# Put your answer here

Not only do all the values you just calculated end in the same fractional component, but also notice that golden_ratio**2 = 1 + golden_ratio. With this information, let鈥檚 figure out how to derive the Golden Angle from the Golden Ratio!

Let f equal the fraction of the length of a circle鈥檚 circumference that is occupied by the arc b, where the ratio of the lengths of the arcs a / b is the Golden Ratio.

golden_ratio = a/b
f = b / (a + b) 
f = (b/b) / ( (a/b) + (b/b) )
f = 1 / (golden_ratio + 1)
f = 1 / golden_ratio**2

From the derivation above, you can see that the fraction of the circumference of the circle occupied by the arc b that is subtended by the Golden Angle is 1 / golden_ratio**2!

In the cell below, approximate the Golden Angle from your approximation of the Golden Ratio in degrees as:

golden_angle = 360*(1/golden_ratio**2)

Your answer should be close to 137.50776405003785.

# Put your answer here

Congratulations!!! You calculated the Golden angle from scratch using computation!!! You will use the Golden angle in the next activity to model the growth of a sunflower.

3.5 While Loops Activity 3: How to Build a Sunflower 馃尰