3.0 La función range¶

La razón dorada calculada con loops 🌻¶

Las plantas exhiben patrones hermosos: desde los patrones de ramificación de los árboles hasta las formas de las hojas y los patrones en espiral de un girasol. Este último patrón, las espirales, surge de la filotaxia (que literalmente significa “hoja” + “arreglo”). La filotaxia es más que el arreglo de las flores de un girasol, es la disposición de todos los órganos laterales (hojas y partes de flores). Hay muchos más patrones además de la espiral, pero para esta lección y la siguiente, nos centraremos en la filotaxia en espiral y trataremos de recrear los patrones inspiradores en las cabezas de girasoles.

¿Cuál es la sucesión de Fibonacci? ¿Cómo se relaciona con los patrones en espiral que se encuentran en los girasoles y en todas las plantas terrestres? La sucesión de Fibonacci es una serie de números que comienza con “0, 1” o “1, 1”. Después de los dos primeros números, el siguiente número se define como la suma de los dos anteriores. Entonces, de 0, 1 surge la sucesión 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,. . ..

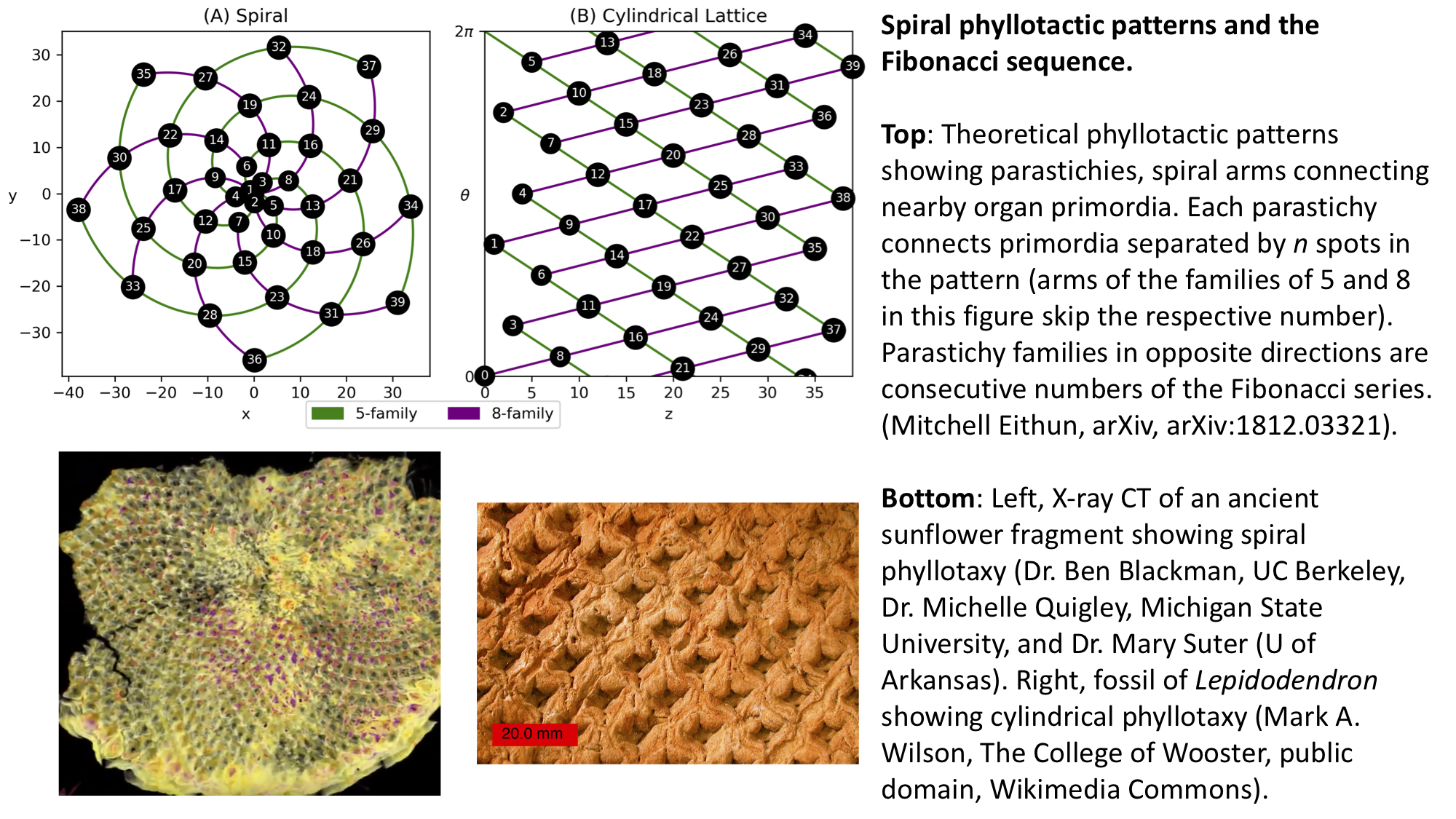
Al observar un girasol, surgen patrones filotácticos en espiral que se proyectan en un disco, patrones de brazos en espiral que emanan del centro. Estos se llaman parastichies y surgen de vecinos cercanos en el patrón filotáctico general que están separados por n primordios secuenciales, donde n es un término de la sucesión de Fibonacci.

Por ejemplo, en una familia parastichy de 5, la espiral surge de conectar cada quinto primordio. Una de las conexiones más fuertes entre la filotaxia y la secuencia de Fibonacci es que las familias parastichy que van en direcciones opuestas son números consecutivos de la sucesión de Fibonacci.

Pero la conexión entre la sucesión de Fibonacci y la filotaxia en espiral es incluso más fuerte que las familias parastichy. La razón dorada (también llamada razón áurea) se puede aproximar como la razón de dos números de Fibbonaci consecutivos. La aproximación se vuelve más precisa a medida que avanzamos en la sucesión. El valor de la razón dorada es $$\varphi=\frac{1 + \sqrt{5}}{2}\approx1.61.$$

Si la circunferencia de un círculo se divide en dos arcos, la razón de cuyas longitudes forman la razón dorada, el ángulo resultante se llama el ángulo dorado. El valor del ángulo dorado es

\[\pi(3 - \sqrt {5})\;\text{radianes ó } 180(3 - \sqrt{5})\approx137.5^\circ.\]

El valor del ángulo entre primordios sucesivos en filotaxia en espiral es el ángulo dorado.

En esta lección aproximaremos los valores de la razón dorada y el ángulo dorado usando loops. En la siguiente actividad, usaremos el valor del ángulo dorado para recrear una cabeza de girasol.

‘Looping’ hacia la razón dorada¶

Las computadoras son realmente buenas para realizar tareas repetitivas. Un loop es una de las principales formas en que le decimos a una computadora que ejecute un fragmento de código una y otra vez.

Los loops vienen de dos maneras:

loops for
loops while

Un loop for iterará sobre un fragmento de código por un número específico de veces. Un loop while seguirá iterando sobre un fragmento de código mientras una condición sea verdadera.

No es estrictamente cierto que el loops simplemente repita lo mismo una y otra vez. Más bien, está iterando sobre un índice. Un índice es un recuento de cuántas veces se repitió el ciclo, 0, 1, 2, 3,... (recordemos que toda la indexación comienza con 0 en python). El índice es un valor que usamos para variar, con cada iteración, lo que hace el loop.

El índice podría ser simplemente un recuento que continúa sucesivamente +1 con cada iteración. O bien usamos el índice para obtener otros valores. Por ejemplo, el índice de un loop podría usarse para iterar sobre los elementos de una lista, que pueden ser cualquier valor que elijamos. Podríamos realizar una función matemática en cada valor del índice del loop para transformarlo en otro conjunto de valores que necesitemos.

Dos formas comunes de iterar sobre un loop son usando la función range () o simplemente una lista. La función range () toma un valor de inicio, parada y paso, o simplemente el valor de parada por sí mismo. Por ejemplo, range (2,10,3) daría como resultado 2,5,8, comenzando en 2 agregando 3 para cada paso hasta detenerse en un valor estrictamente menor a 10. También podemos proporcionar simplemente un valor de parada para el rango. Por ejemplo, range(3) produciría 0,1,2. Es importante recordar con range () que el inicio es inclusivo y la parada es exclusiva.

Los loops for tienen una estructura estricta, en la que se proporciona un nombre arbitrario para la variable iterable, y un conjunto de valores sobre los que iterar esa variable. La primera línea termina en un : y el código dentro del loop está sangrado. Python es sensible tanto al : como a la sangría. Por ejemplo:

for i in range(start, stop, step):
    # Tu código aquí
    # Usemos print mientras tanto
    print(i)
    
for val in my_list:
    # Tu código aquí
    # Usemos print mientras tanto
    print(val)

A diferencia de un loop for, un loop while seguirá iterando mientras una condición sea verdadera y dejará de iterar cuando dicha condición ya no lo sea. Una forma común de estructurar un loop while es agregar un contador. Un contador es una variable fuera del ciclo que aumentará su valor cada vez que se ejecute el ciclo.

Configuramos un loop while para que se ejecute hasta que el contador supere un cierto valor. El valor del contador aumenta con el signo +=, que es equivalente a counter = counter + 1 en el ejemplo que se muestra a continuación. Una forma de pensar en += es que agrega un valor al valor anterior del contador para llegar a un nuevo valor de contador.

A continuación se muestra un ejemplo de un loop while con un contador:

counter = 0

while counter < 20:
    # Tu código aquí
    # Usemos print mientras tanto
    print(counter)
    # Incrementemos el counter cada vez que el loop itera
    counter += 1

Vale la pena invertir algo de tiempo en comprender los loops ¡son un elemento clave de la codificación en python! Los loops se vuelven muy poderosos cuando se usan inteligentemente con el código dentro de ellos, y también al crear valores y listas fuera de los loops que los loops modifican a medida que se ejecutan.

Prestemos atención a la forma en que se usan los loops en el tutorial a continuación, y cómo se pueden usar para calcular algo como la sucesión de Fibonacci.

🐍 Objetivos de aprendizaje de python¶

La función range () y cómo ésta produce una sucesión de enteros para iterar en un loop (1:20)
Cómo escribir un loop for (2:40)
Cómo utilizar el signo += en un contador (7:25)
Cómo crear una lista vacía fuera de un loop y llenarla con resultados del loop (13:09)
Cómo utilizar un loop for para calcular la suceción de Fibonacci (20:33)
Cómo escribir un loop while usando un contador (26:29)

🌻 Objetivos de aprendizaje de plantas¶

¡Las plantas son computadoras!
Éstas producen resultados de forma iterativa (como hojas y flores), al igual que lo hacen los loops.
El modelado computacional intenta replicar fenómenos de la naturaleza. Ningún modelo es perfecto.
El ángulo dorado que usan las plantas y que calcularemos se basa en matemáticas computacionales.
Usaremos los girasoles y el ángulo dorado como inspiración para aprender de las plantas.

La función `range()` y cómo ésta produce una sucesión de enteros para iterar en un loop¶

Mira este video de 0:00 a 2:35

Para español, haga click en configuración, seleccione “español” debajo de los subtítulos.

Traducción por Erik Amézquita (Michigan State University)

# Para reproducir el siguiente tutorial, presiona shift + enter

from IPython.display import YouTubeVideo
from datetime import timedelta
start=int(timedelta(hours=0, minutes=0, seconds=0).total_seconds())
end=int(timedelta(hours=0, minutes=2, seconds=35).total_seconds())

YouTubeVideo("Cvi3dByz9SE",start=start,end=end,width=640,height=360)

La siguiente es una transcripción del video.

Empecemos entonces. Empezaremos con la función range() y cómo se usa para producir una sucesión de enteros sobre los que iteramos en un loop.

Este es un buen momento para repasar la función de ayuda. Si tenemos algunas dudas sobre qué hace cierta función, podemos simplemente escribir el signo ? delante de ella. Si presionamos Shift + Enter, obtenemos un pequeño cuadro de ayuda. Puede no ser tan útil, pero intentará decirte algo. Por ejemplo, podemos ver que las entradas a la función range() son inicio, parada y paso. Esto es muy parecido a indexación y segmentación que hemos aprendido antes y dice que devuelve un objeto que produce una secuencia de enteros desde el inicio, inclusivo, hasta el final, exclusivo, con tamaño de paso. Y esto casi suena exactamente como la indexación y el corte que aprendimos antes.

# ¿Qué es la función range ()?
# Si tiene alguna duda, utilice la función de ayuda con un "?"

?range 

# range(start, stop[, step]) -> range object
# Return an object that produces a sequence of integers
# from start (inclusive) to stop (exclusive) by step.  
# range(i, j) produces i, i+1, i+2, ..., j-1
# start defaults to 0, and stop is omitted! 
# range(4) produces 0, 1, 2, 3
# These are exactly the valid indices for a list of 4 elements
# When step is given, it specifies the increment (or decrement)

Basado en ello intentemos ejecutar una función range(). Pongamos el número 8. Quizás basado en nuestra indexación anterior esperaríamos que nos devolviese 0, 1, 2, 3, 4, 5, 6, 7. Pero ese no es el caso. En cambio, solo nos da un rango de 0 a 8, que es algo de que esperaríamos basándonos en poner 8 allí. Y bueno, esto es un poco inesperado.

Así que exploremos más, y como veremos, range() solo funciona realmente en el contexto de un loop.

# ¡Así que probemos la función de rango!

print(range(8))

range(0, 8)

Welcome / Bienvenid@ 3.1 Loops for

Plants & Python